Robotic Maze Solving Tutorial
Intro
Well you could say that I have been playing around with maze solving for a while. After three robots, I finally accomplished it. I am going to try and share with you what I did.
Left Hand On The Wall Algorithm
What are the steps In maze solving? There are basically 2 steps. The first is to drive through the maze and find the end of it. The second is to optimize that path so your robot can travel back through the maze, but do it perfectly with out going down any dead ends.
How does the robot find the end of the maze? I use a technique called "the left hand on the wall" algorithm. Imagine you are in a maze and you keep your left hand on a the edge of the wall at all times. Doing this would eventually get you out of a non-looping maze. This tutorial will only deal with mazes that do not contain cycles.
This left hand on wall algorithm can be simplified into these conditions:
- If you can turn left then turn left
- Else if you can continue driving straight then drive straight
- Else if you can turn right then turn right
- If you are at a dead end then turn around
The robot has to make these decisions when at an intersection. An intersection is any point on the maze where you have the opportunity to turn. If the robot comes across an opportunity to turn and does not turn then this is consider going straight. Each move taken at an intersection or when turning around has to be stored.
Here is the shorthand I will use for these decisions:
- L = left turn
- R = right turn
- S = going straight
- B = turning around
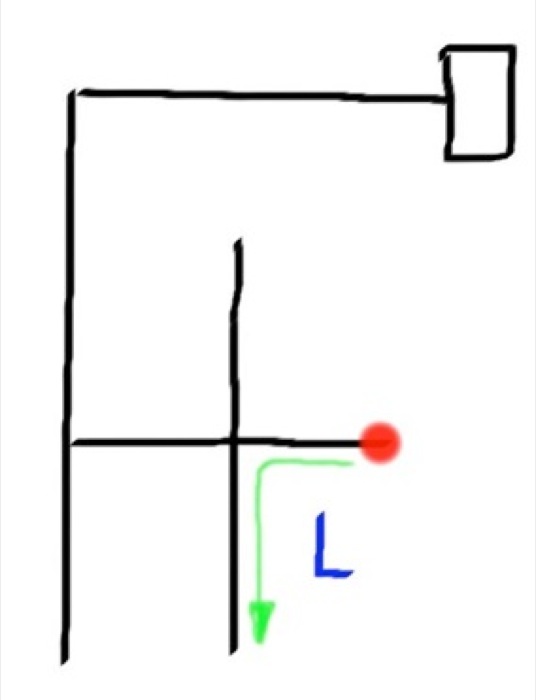
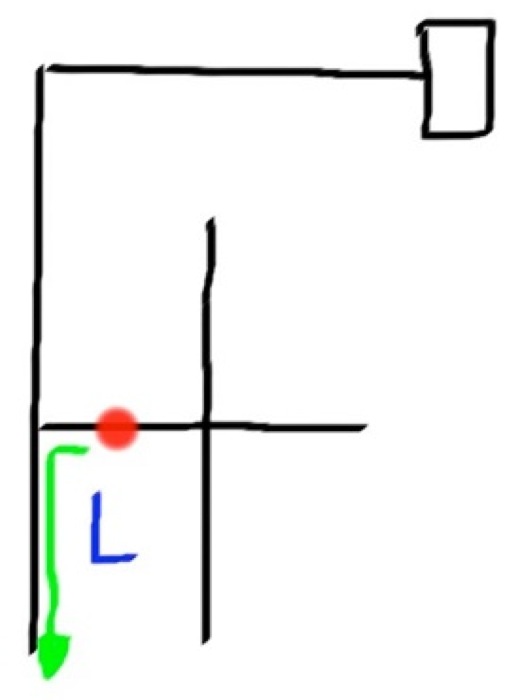
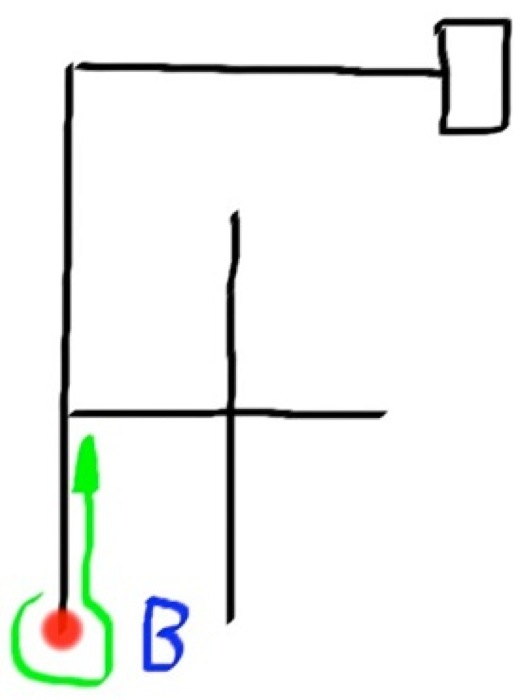
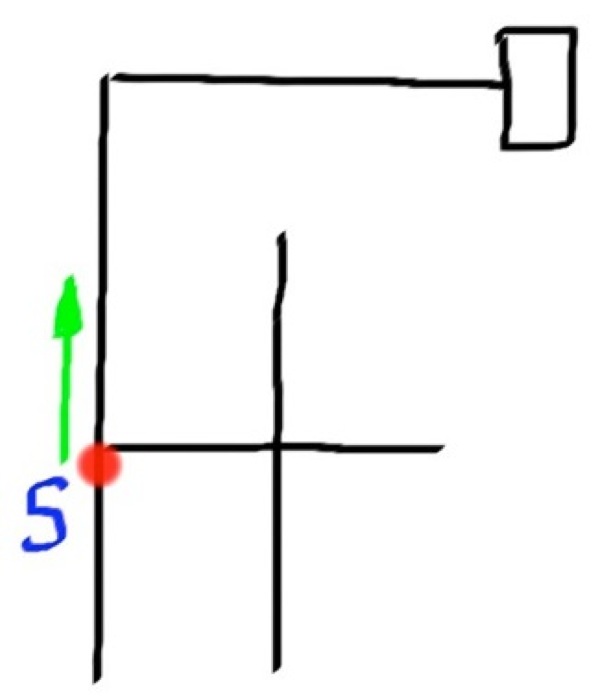
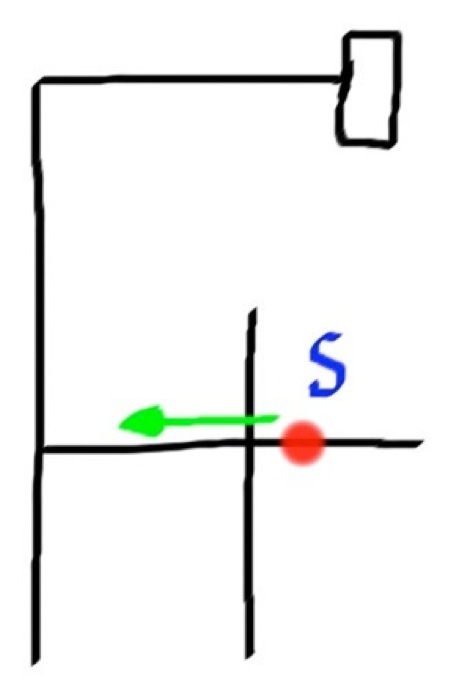
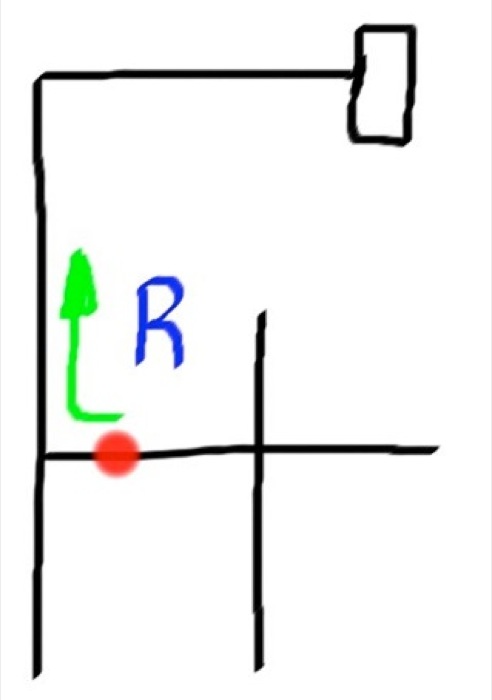
So let me apply this method to a simple maze and see if you can follow it. The red circle will be the robot.
Final Path = LBLLBSR
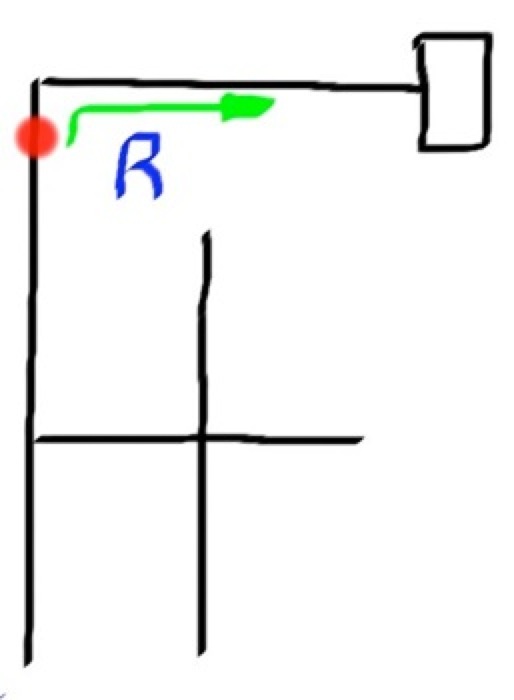
I hope you were able to see how those moves are made using the left hand on the wall technique. This can be applied to any non-looping maze.
Shortest Path
Ok so now you have a path. In this case it is "LBLLBSR", but how does the robot change that into the correct path? Well let's take a look at what the correct path would be.
Final Path = SRR
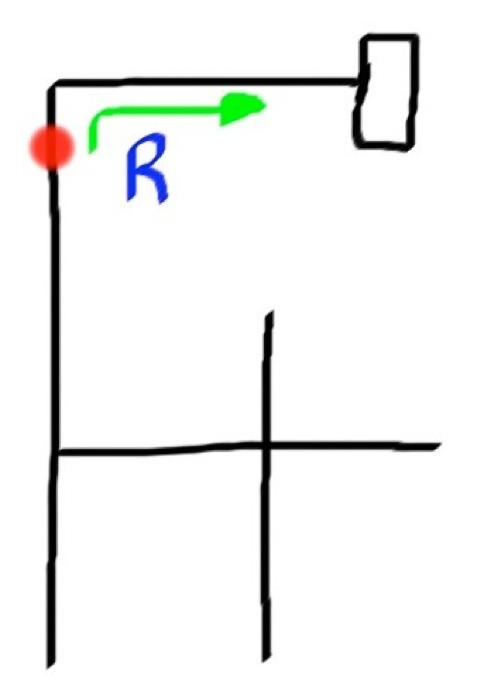
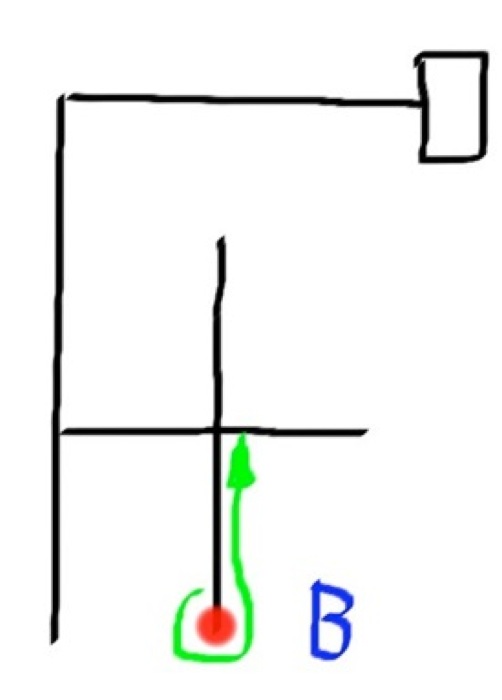
So we need our path to go from "LBLLBSR" to the shortest path, which is "SRR". To start off we look at where we went wrong. A "B" indicates the robot turned around - meaning it went down the wrong path. To optimize the path we have to get rid of the "B" by using some substitution.
Lets look at the first 3 moves in the path. These moves are "LBL". That move looks like this:
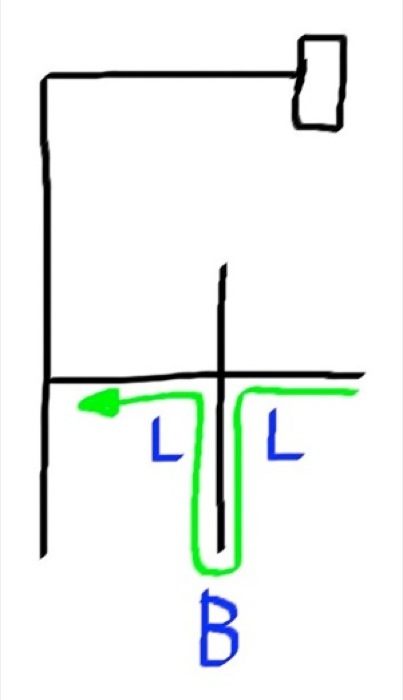
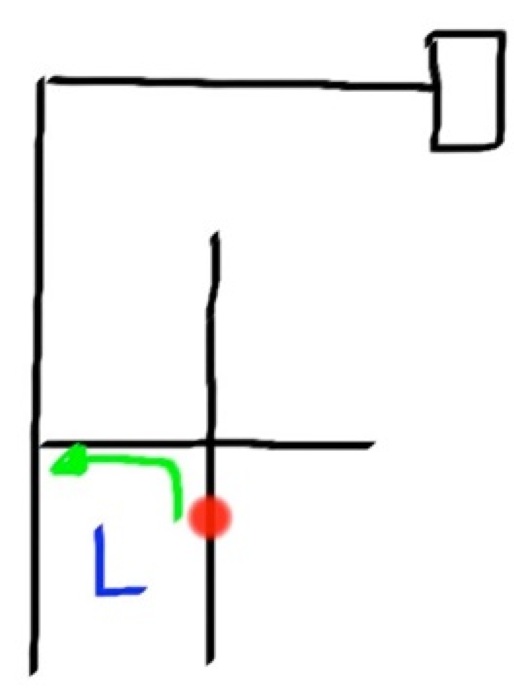
Instead of turning left, then turning around, and turning left again, the robot should have gone straight. So we can say that LBL = S. This substitution is what the robot uses to optimize the path. That is one example but here is the whole list:
- LBR = B
- LBS = R
- RBL = B
- SBL = R
- SBS = B
- LBL = S
You may not come across all of these when maze solving, but they are required when optimizing the path. Some even put "B" back into the path. This is required to further optimize the path correctly. You can figure out why for yourself or just trust me.
Let's optimize our path now that we know how to:
Path = LBLLBSR
LBL = S so our new path would be: SLBSR
We also know LBS = R so our new path would be: SRR
As you can see we got the path that we were looking for.
My robot optimizes the path as it travels. The path is stored in an array and every time it goes to store a new move it checks to see if the previous move was a "B", if it was then it optimizes the path. You need to know at least 3 moves to optimize the path - the move before and after the turn around (and the turn around itself).
Another Example
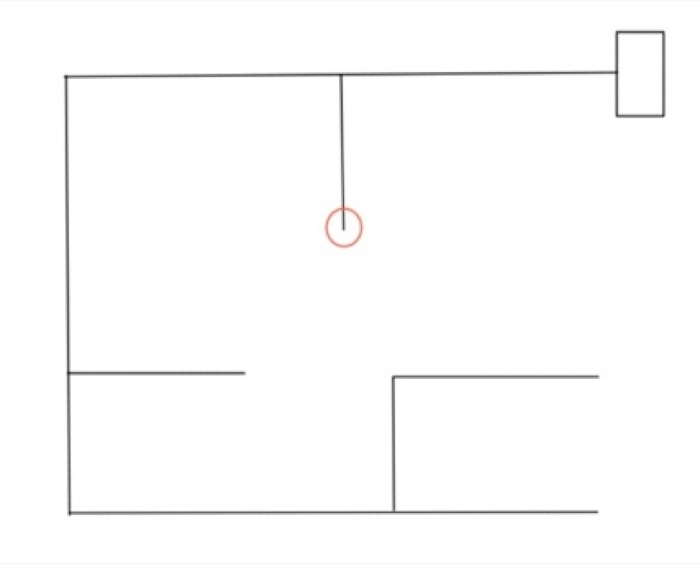
Using the left hand on the wall algorithm, here is the path the robot would take: LLLBLLLRBLLBSRSRS
Now here is the process of shortening that path: LL(LBL = S)LL(RBL = B)(LBS = R)RSRS
The new path would be: LLSLLBRRSRS
Continue shortening it until all the “B”s are gone: LLSL(LBR = B)RSRS
The new path would be: LLSLBRSRS
Continue shortening it: LLS(LBR = B)SRS
The new path would be: LLSBSRS
Continue shortening it: LL(SBS = B)RS
The new path would be: LLBRS
Continue shortening it: L(LBR = B)S
The new path would be: LBS
The final path is: LBS = R
Implementation Details
I ran into some trouble programming my robot because I used an array of sensors that are all collinear. The problem with this is that different intersections may look alike. So my robot goes forward a bit every time it detects an intersection so it can see what is after that intersection. The prime example is when there is a right turn. If you can go straight instead of turning right then you should, but the only way to know if you can go straight is to drive forward and see if the line continues on.
You will also need a function that drives the robot in a relatively straight line. So it needs to do some line following also. That is why a maze robot generally has 4, 5, or 6 sensors.
I used some other techniques for completing turns without encoders, but this is getting too far away from maze solving and more into general practice. To cut it short, you will need some really good programming to keep your robot on the line well enough to read the sensors correctly and to correctly identify intersections.